Ligang Sun, M. Sc.
Main Supervisor: I. Neumann; Co-Supervisor: S. Schön
This project deals with the development of methods and procedures for reliable solutions with integrity measures for dynamic sensor networks in which both the observations and the system knowledge are superimposed by random and unknown but bounded (UBB) uncertainties. For this purpose, the nonlinear observation and system equation of the filter are extended to the imprecise case and solved by methods considering both random and UBB uncertainties. This includes the extension of the available basic concepts by elements of guaranteed parameter estimation as well as filtering for merging the knowledge from observation and about the system. A particular focus of this project is on the propagation of imprecision, with the goal of significantly solving the problem of overestimation, which usually occurs with interval mathematics when finding suitable reformulations. These contents are transferred to selected multi-sensor systems in the experimental laboratory. As input values, measurements collected in projects of the Geodetic Institute can be used. Real measurements as well as measurements with superior accuracy of a reference measurement system are available, which data may serve for the validation of the methods.
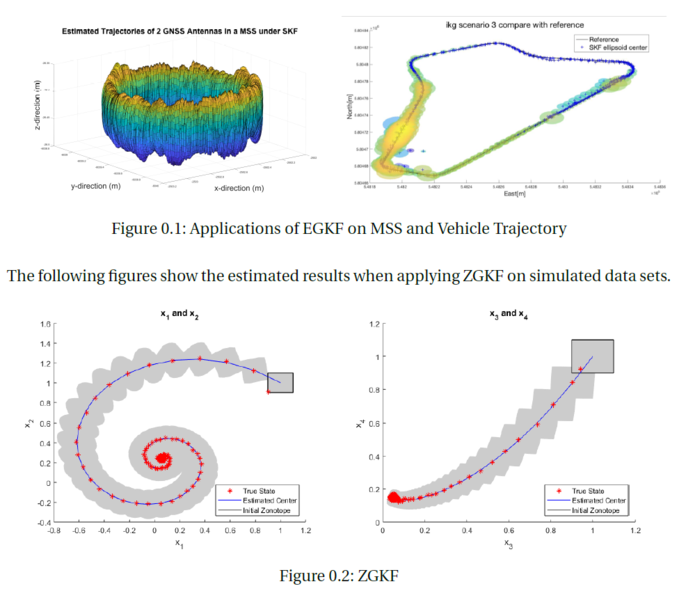
Currently we developed two set-based filteringmodels: Ellipsoidal and Gaussian Kalman Filter (EGKF) for discrete-time nonlinear systems and Zonotopic and Gaussian Kalman Filter (ZGKF) for hybrid LTI systems. Here are the estimated results when applying EGKF onmulti-sensor system (MSS) and Mapathon data sets.
The future work includes the applications of these set-based filtering models on real data sets, e.g., state estimation for multi-sensor system or overtaking strategies for autonomous vehicles.